EL MÉTODO

 

Los casos relacionados con cuerpos rígidos y fuerzas en equilibrio han sido el antecedente para conocer ahora acerca de las armaduras, que no son otra cosa que estructuras formadas por elementos rígidos unidos entre sí.

 En estos casos se determinarán las fuerzas externas que actúan sobre la estructura y se analizarán las fuerzas internas que mantienen unidas sus partes.

 

En el contenido de éste tema podrás encontrar imágenes ilustrativas, videos, ejemplos y aplicaciones del análisis estructural. Está diseñado con recursos de varios autores, compilado y resumido de manera que puedas realizar el análisis de estructuras por el método de los nodos siempre comprendiendo el objetivo final del cálculo de las fuerzas, comencemos con las definiciones de los elementos que se utilizarán:

Armadura: Es un tipo de estructura de mayor importancia en ingeniería. Proporciona soluciones tanto prácticas como económicas a muchos problemas, principalmente en el diseño de puentes y edificios. Las armaduras que a continuación vamos a analizar se tratan de estructuras planas en dos dimensiones, pero que,  varios planos unidos entre sí pueden formar elementos tridimensionales. Una armadura consta de:

 Miembros:  Son  los elementos rectos conectados entre sí por medio de nodos o nudos. Por lo general, los miembros de una armadura son delgados y pueden soportar poca carga lateral, por lo tanto, las cargas deben aplicarse sobre los nudos y no directamente sobre los miembros. De esta teoría suponemos que todos los miembros sólo son sometidos a cargas de compresión o tensión a lo largo de su eje, y de eso se trata el análisis, de encontrar las magnitudes de la tensión o compresión de cada miembro.

 Nodos: Son las conexiones entre cada miembro. Las fuerzas que actúan sobre ellos se reducen a un solo punto, porque son las mismas fuerzas transmitidas desde los ejes de los miembros. A través de los nodos nunca se puede atravesar un miembro. Las conexiones en los nudos están formadas usualmente por pernos o soldadura en los extremos de los miembros unidos a una placa común llamada placa de unión.

 

Apoyos: Toda estructura necesariamente debe estar apoyada en uno o más puntos, los cuales se llaman puntos de apoyo, y como transmiten su carga a través de esos puntos, en el diagrama de fuerzas debemos considerar los vectores que indiquen las reacciones en esos apoyos.  Cada diferente tipo de apoyo generará  a su vez un tipo de 

Reacción: Son las fuerzas generadas en los apoyos, son opuestas en dirección de las fuerzas de la estructura que actúan en ese punto, existen tres tipos de reacciones:

   

    Reacciones equivalentes a una fuerza con línea de acción conocida. Generadas por apoyos tipo: patines o rodamientos, balancines, superficies sin fricción, eslabones y cables cortos, collarines sobre barras sin fricción y pernos en ranuras lisas. En las reacciones de éste tipo hay una sola incógnita 

    

    Reacciones equivalentes a una fuerza de dirección desconocida. Generadas por pernos lisos en orificios ajustados, articulaciones y superficies rugosas. En las reacciones de este grupo intervienen dos incógnitas.

   

        Reacciones equivalentes a una fuerza y a un par. Producidas por soportes fijos que impiden cualquier movimiento del cuerpo inmovilizándolo por completo y obligándolo a reaccionar con tres fuerzas incógnitas (dos componentes de traslación y un momento).

 Equilibrio: Cuando las fuerzas y el par son ambos iguales a cero forman un sistema equivalente nulo se dice que el cuerpo rígido está en equilibrio.

 Por consiguiente, las condiciones necesarias y suficientes para el equilibrio de un cuerpo rígido pueden obtenerse haciendo R y MRO iguales a cero.

 

Descomponiendo cada fuerza y cada momento en sus componentes rectangulares,  podemos expresar las condiciones necesarias y suficientes para el equilibrio de un cuerpo rígido por medio de las seis ecuaciones escalares siguientes:

 

Las ecuaciones obtenidas pueden usarse para determinar las fuerzas desconocidas aplicadas a cuerpos rígidos o las reacciones desconocidas que ejercen sobre éste sus apoyos. Notamos que las primeras tres ecuaciones expresan el hecho de que las fuerzas en X, Y y Z están equilibradas; las otras tres ecuaciones indican que los momentos con respecto a los tres ejes X, Y y Z también están equilibrados, o sea, ni se va a mover hacia ninguna parte y tampoco va a girar en ningún sentido, el cuerpo está en equilibrio.

Cada caso presenta diferencias, pero la tarea principal es despejar de las seis ecuaciones anteriores la mayor cantidad de variables posibles, a partir del diagrama de fuerzas. 

 

 

Por lo tanto el diagrama de fuerzas es la clave para el planteamiento correcto de las ecuaciones y el cálculo exacto de cada fuerza en cada nudo. Veamos los siguientes ejemplos:

 

PROBLEMA 1.           Usando el método de los nudos, determine la fuerza en cada miembro de la armadura que se muestra:

 El primer paso será representar el diagrama de fuerzas de la armadura completa, dibujando todos los vectores que afectan a la armadura y sin olvidar las reacciones en los apoyos. Es importante también colocar las medidas conocidas de cada miembro y las magnitudes de los vectores de cada fuerza.

 Como la condición para que existan las armaduras es su estabilidad, recordamos que tenemos que aplicar las ecuaciones de la suma de todas las fuerzas  y todos los momentos e igualarlos a cero. Sería conveniente comenzar por un nodo donde sólo exista una incógnita; la ecuación del momento en el nodo C nos podría dar el valor del vector que genera la reacción en el apoyo E. Porque automáticamente se eliminan las fuerzas Cx y Cy, puesto que no provocan ningún giro en C

 Enseguida podemos darnos cuenta de que la sumatoria de fuerzas en X implica un solo vector, por lo que su ecuación tendrá una sola incógnita. Y será fácil su deducción:

 Una vez que conocemos la magnitud en la reacción del nodo E, nos damos cuenta de que la ecuación que incluye a las fuerzas en el sentido vertical (Y) sólo tendrá una incógnita, por lo que procedemos a resolverla para encontrar el vector generado por la reacción vertical en el nodo C.

 

Y entonces, ahora sí procedemos a calcular las fuerzas en cada nodo.

 Comencemos con el nodo A.

En primer lugar vamos a dibujar el diagrama de fuerzas que conocemos que intervienen en este nodo, dejando con líneas punteadas los vectores de los miembros que todavía no conocemos.

  Enseguida hacemos un polígono de fuerzas en equilibrio, es decir, un polígono con los vectores involucrados en el nodo, acomodados de punta a cola, de tal manera que se cierre el polígono. Sólo existe una combinación para equilibrar triángulos.

 Con las medidas de los miembros podemos deducir el ángulo de inclinación de éstos y por lo tanto es el mismo ángulo de inclinación de los vectores. La función tangente nos servirá para encontrar el ángulo de inclinación.

 Y como conocemos el valor del vector que está aplicado verticalmente en A, y tenemos el ángulo, podemos fácilmente conocer  la magnitud de cualquiera de los otros dos vectores, utilizando las funciones seno, coseno y/o tangente.

 Ahora, mediante la observación únicamente, deduciremos el sentido de los vectores recién encontrados. El vector FAB se dirige hacia la derecha, si lo trasladáramos al diagrama de fuerzas (en la línea punteada) podemos darnos cuenta de que “tira” del nodo A, por lo tanto deducimos que el miembro está en tensión.

 Así mismo si trasladamos el vector del polígono en equilibrio al diagrama de fuerzas, podemos ver que el vector FAD “presiona” al nodo, por lo que deducimos que está en compresión.

 

Ahora continuaremos con el nodo D:

En primer lugar vamos a dibujar el diagrama de fuerzas que conocemos que intervienen en este nodo, dejando con líneas punteadas los vectores de los miembros que todavía no conocemos, pero la ventaja es que ahora sí conocemos una de las fuerzas de los miembros, la que fue calculada en el nodo A: FAD = 2,500 lb en compresión. Quedan dos fuerzas sin determinar, por lo que las dejamos como líneas punteadas.

 Enseguida dibujamos el polígono de fuerzas en equilibrio para el nodo D, donde inciden tres vectores, uno de ellos conocido, recordemos que la condición de equilibrio se cumple si los vectores se acomodan de punta a cola.

 Con las medidas de los miembros podemos obtener los ángulos internos del triángulo, y con la ley de los senos, podremos encontrar las magnitudes de los vectores que faltan.

Ahora, mediante la observación únicamente, deduciremos el sentido de los vectores recién encontrados. El vector FDB se dirige hacia arriba a la derecha, si lo trasladáramos al diagrama de fuerzas (en la línea punteada) podemos darnos cuenta de que “tira” del nodo A, por lo tanto deducimos que el miembro está en tensión.

 Así mismo si trasladamos el vector del polígono en equilibrio al diagrama de fuerzas, podemos ver que el vector FED “presiona” al nodo, por lo que deducimos que está en compresión.

 

Ahora continuaremos con el nodo B:

En primer lugar vamos a dibujar el diagrama de fuerzas que conocemos que intervienen en este nodo, dejando con líneas punteadas los vectores de los miembros que todavía no conocemos, pero la ventaja es que ahora ya conocemos tres de las fuerzas involucradas, las que fueron calculadas en el nodo A y en el nodo D. Quedan dos fuerzas sin determinar, por lo que las dejamos como líneas punteadas.

 Es importante dibujar el vector de la carga vertical del nodo hacia abajo, para evitar confusiones.

 Enseguida dibujamos los vectores faltantes, suponiendo arbitrariamente que los miembros están en tensión, esto es, que están “tirando” del nodo B.

 Las fuerzas que no son horizontales o verticales (es decir, todas las inclinadas) deberán descomponerse en sus dos componentes X y Y, utilizando las funciones seno, coseno y tangente. Primero que nada, se deducirán los ángulos de los vectores inclinados.

 

Ahora se dibujan dos vectores rectangulares en vez de cada uno de los vectores inclinados, de esa manera tendremos en el diagrama de fuerzas solamente fuerzas verticales y horizontales, por lo que ya podemos aplicar las ecuaciones del equilibrio. 

 

Comenzamos con la sumatoria de fuerzas en Y, de donde podemos deducir la magnitud del vector FBE

 Inmediatamente nos damos cuenta de que el miembro está en compresión, porque fue arbitrariamente dibujado en tensión, y el resultado fue negativo, por lo tanto el miembro está en compresión.

 Ahora continuamos con la ecuación donde sumamos todas las fuerzas en X, de ahí deduciremos la magnitud del vector FBC.

 También podemos observar que este miembro sí está en tensión, pues el resultado obtenido es de signo positivo. Vamos bien.

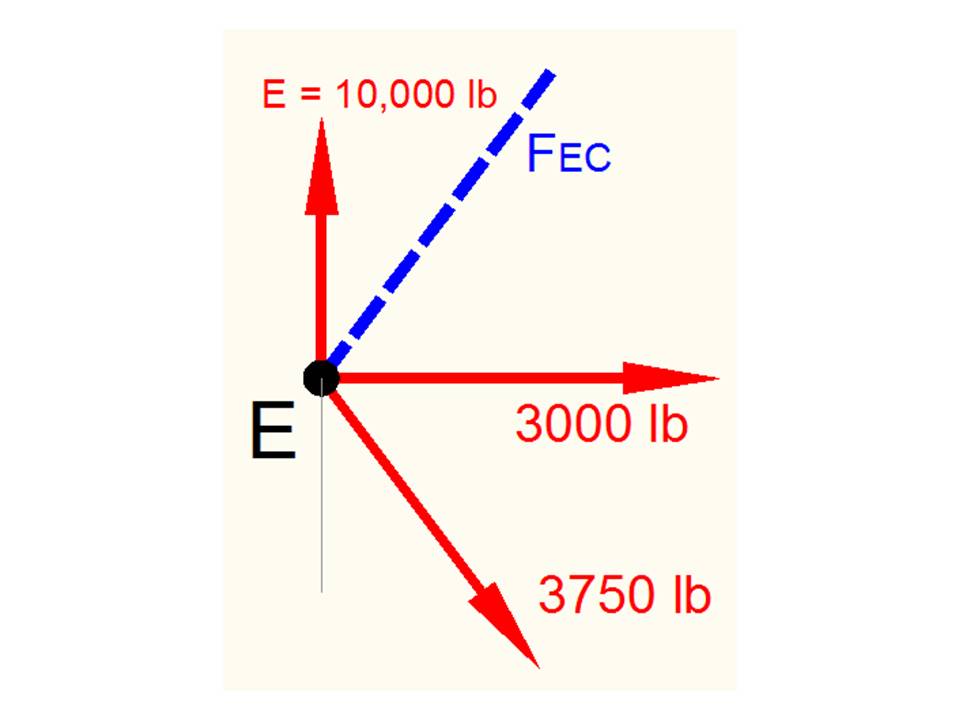
 Ahora vamos a calcular los vectores del nodo E. Dibujemos el diagrama de fuerzas de los vectores que inciden en C, de los cuales conocemos 3, sólo existe una incógnita, la cual es FEC, la cual también será incluida en el diagrama de fuerzas, la supondremos arbitrariamente a tensión,  el resultado nos comprobará si fue buena la suposición.

 Como los vectores FBE y FDE y la reacción E “presionan” al nodo E, podemos pasarlos del otro lado del nodo, lo cual nos facilitará la comprensión del diagrama de fuerzas y no lo afecta para nada.

 Dibujamos el vector desconocido FEC, suponiendo arbitrariamente que está en tensión.

 Calculamos los ángulos con las medidas de los miembros y la función tangente.

 Con la aplicación de la ecuación de la sumatoria de las fuerzas en X, podemos deducir la magnitud de FEC. La cual resulta negativa, lo que quiere decir que la fuerza realmente está en compresión, al contrario de cómo fue supuesta antes de hacer el cálculo.

 Aplicando la ecuación de la sumatoria de las fuerzas en Y nos permite verificar los resultados de la ecuación (que debe resultar cero).

 Ya por último resta el nodo C; con los valores obtenidos en los otros nodos para los vectores FBC y FEC, y los valores de las reacciones obtenidas al principio del problema podemos dibujar el diagrama de fuerzas en el nodo C. No olvidemos anotar las medidas conocidas de los miembros.

 Recordemos que los vectores que inciden en compresión al nodo, deben pasarse del otro lado del nodo, en la misma línea de acción, para evitar confusiones.

 Enseguida se proceden a calcular los ángulos de inclinación de los miembros inclinados (no horizontales ni verticales).

 Se sustituyen los vectores inclinados por dos componentes rectangulares (en X y Y).

 Ahora se procede a aplicar la ecuación de las fuerzas en X, como conocemos todos los valores, simplemente nos sirve de comprobación.

 Lo mismo hacemos con la ecuación de las fuerzas en Y. También para comprobar.

 

Videos que pueden ayudarnos a la comprensión del tema: